We can't find the internet
Attempting to reconnect
Something went wrong!
Hang in there while we get back on track
Joshua Potter
Tagless Final Parsing
25 Dec 2021
In his introductory text, Oleg Kiselyov discusses the tagless final strategy for implementing DSLs. The approach permits leveraging the strong typing provided by some host language in a performant way. This post combines key thoughts from a selection of papers and code written on the topic. We conclude with an implementation of an interpreter for a toy language that runs quickly, remains strongly-typed, and can be extended without modification.
Introduction
To get started, let’s write what our toy language will look like.
digit = ? any number between 0-9 ? ;
(* We ignore any leading 0s *)
integer = digit, { digit } ;
e_integer = [ e_integer, ("+" | "-") ]
, ( "(", e_integer, ")" | integer )
;
boolean = "true" | "false" ;
e_boolean = [ e_boolean, ("&&" | "||") ]
, ( "(", e_boolean, ")" | boolean )
;
expr = e_integer | e_boolean ;The above expresses addition, subtraction, conjunction, and
disjunction, to be interpreted in the standard way. All operations are
left-associative, with default precedence disrupted via parenthesis
(()). Our goal is to use megaparsec
to interpret programs in this language, raising errors on malformed or
invalidly-typed inputs. We will evaluate interpreter performance on
inputs such as those generated by
echo {1..10000000} | sed 's/ / + /g' > input.txtTo support inputs like above, ideally we mix lazy and strict functionality. For example, we should lazily load in a file but strictly evaluate its contents. Certain languages struggle without this more nuanced evaluation strategy, e.g.
$ (echo -n 'print(' && echo -n {1..10000000} && echo ')') |
sed 's/ / + /g' > input.py
$ python3 input.py
Segmentation fault: 11Note it’d actually be more efficient on our end to not use megaparsec at all! The library loads in the entirety of to-be-parsed text into memory, but using it will hopefully be more representative of projects out in the wild.
Initial Encoding
How might we instinctively choose to tackle an interpreter of our language? As one might expect, megaparsec already has all the tooling needed to parse expressions. We can represent our expressions and results straightforwardly like so:
data Expr
= EInt Integer
| EBool Bool
| EAdd Expr Expr
| ESub Expr Expr
| EAnd Expr Expr
| EOr Expr Expr
deriving (Show)
data Result = RInt Integer | RBool Bool deriving (Eq)We use a standard ADT to describe the structure of our program,
nesting the same data type recursively to represent precedence. For
instance, we would expect a (so-far fictional) function
parse to give us
>>> parse "1 + 2 + 3"
EAdd (EAdd (EInt 1) (EInt 2)) (EInt 3)We can then evaluate expressions within our Expr type.
Notice we must wrap our result within some Error-like
monad considering the ADT does not necessarily correspond to a
well-typed expression in our language.
asInt :: Result -> Either Text Integer
asInt (RInt e) = pure e
asInt _ = Left "Could not cast integer."
asBool :: Result -> Either Text Bool
asBool (RBool e) = pure e
asBool _ = Left "Could not cast boolean."
toResult :: Expr -> Either Text Result
toResult (EInt e) = pure $ RInt e
toResult (EBool e) = pure $ RBool e
toResult (EAdd lhs rhs) = do
lhs' <- toResult lhs >>= asInt
rhs' <- toResult rhs >>= asInt
pure $ RInt (lhs' + rhs')
toResult (ESub lhs rhs) = do
lhs' <- toResult lhs >>= asInt
rhs' <- toResult rhs >>= asInt
pure $ RInt (lhs' - rhs')
toResult (EAnd lhs rhs) = do
lhs' <- toResult lhs >>= asBool
rhs' <- toResult rhs >>= asBool
pure $ RBool (lhs' && rhs')
toResult (EOr lhs rhs) = do
lhs' <- toResult lhs >>= asBool
rhs' <- toResult rhs >>= asBool
pure $ RBool (lhs' || rhs')With the above in place, we can begin fleshing out our first parsing attempt. A naive solution may look as follows:
parseNaive :: Parser Result
parseNaive = expr >>= either (fail . unpack) pure . toResult
where
expr = E.makeExprParser term
[ [binary "+" EAdd, binary "-" ESub]
, [binary "&&" EAnd, binary "||" EOr]
]
binary name f = E.InfixL (f <$ symbol name)
term = parens expr <|> EInt <$> integer <|> EBool <$> booleanThere are certainly components of the above implementation that
raises eyebrows (at least in the context of large inputs), but that
could potentially be overlooked depending on how well it runs. Running
parseNaive1 against input.txt
shows little promise though:
$ cabal run --enable-profiling exe:initial-encoding -- input.txt +RTS -s
50000005000000
...
4126 MiB total memory in use (0 MB lost due to fragmentation)
...
Total time 25.541s ( 27.121s elapsed)
...
Productivity 82.3% of total user, 78.9% of total elapsedA few immediate takeaways from this exercise:
This solution
- has to run through the generated AST twice. First to build the AST
and second to type-check and evaluate the code
(i.e.
toResult). - is resource intensive. It consumes a large amount of memory
(approximately
4GiB in the above run) and is far too slow. A stream of 10,000,000 integers should be quick and cheap to sum together. - is unsafe. Packaged as a library, there are no typing guarantees
we leverage from our host language. For example, expression
EAnd (EInt 1) (EInt 2)is valid. - suffers from the expression problem. Developers cannot extend our language with new operations without having to modify the source.
Let’s tackle each of these problems in turn.
Single Pass
Our naive attempt separated parsing from evaluation because they
fail in different ways. The former raises a
ParseErrorBundle on invalid input while the latter raises
a Text on mismatched types. Ideally we would have a
single error type shared by both of these failure modes.
Unfortunately, this is not so simple - the Operator types
found within makeExprParser have incompatible function
signatures. In particular, InfixL is defined as
InfixL :: m (a -> a -> a) -> Operator m ainstead of
InfixL :: (a -> a -> m a) -> Operator m aTo work around these limitations, we define our binary functions to
operate and return on values of type Either Text Expr. We
then raise a Left on type mismatch, deferring error
reporting at the Parser level until the current
expression is fully parsed:
parseSingle :: Parser Result
parseSingle = expr >>= either (fail . unpack) pure
where
expr = E.makeExprParser term
[ [binary "+" asInt EInt EAdd, binary "-" asInt EInt ESub]
, [binary "&&" asBool EBool EAnd, binary "||" asBool EBool EOr ]
]
binary name cast f bin = E.InfixL do
void $ symbol name
pure $ \lhs rhs -> do
lhs' <- lhs >>= cast
rhs' <- rhs >>= cast
toResult $ bin (f lhs') (f rhs')
term = parens expr <|>
Right . RInt <$> integer <|>
Right . RBool <$> booleanResource Usage
Though our above strategy avoids two explicit passes
through the AST, laziness sets it up so that we build this intertwined
callstack without actually evaluating anything until we interpret the
returned Result. The generated runtime statistics are
actually worse as a result:
cabal run --enable-profiling exe:initial-encoding -- \
input.txt -m single +RTS -sWe’ll use a heap profile to make the implementation’s shortcomings more obvious:
cabal run --enable-profiling exe:initial-encoding -- \
input.txt -m single +RTS -hrTo iterate faster, reduce the number of integers in
input.txt. The resulting heap profile should remain
proportional to the original. Just make sure the program runs for long
enough to actually perform meaningful profiling. This section works on
inputs of 100,000 integers.
The generated heap profile, broken down by retainer set, looks as follows:
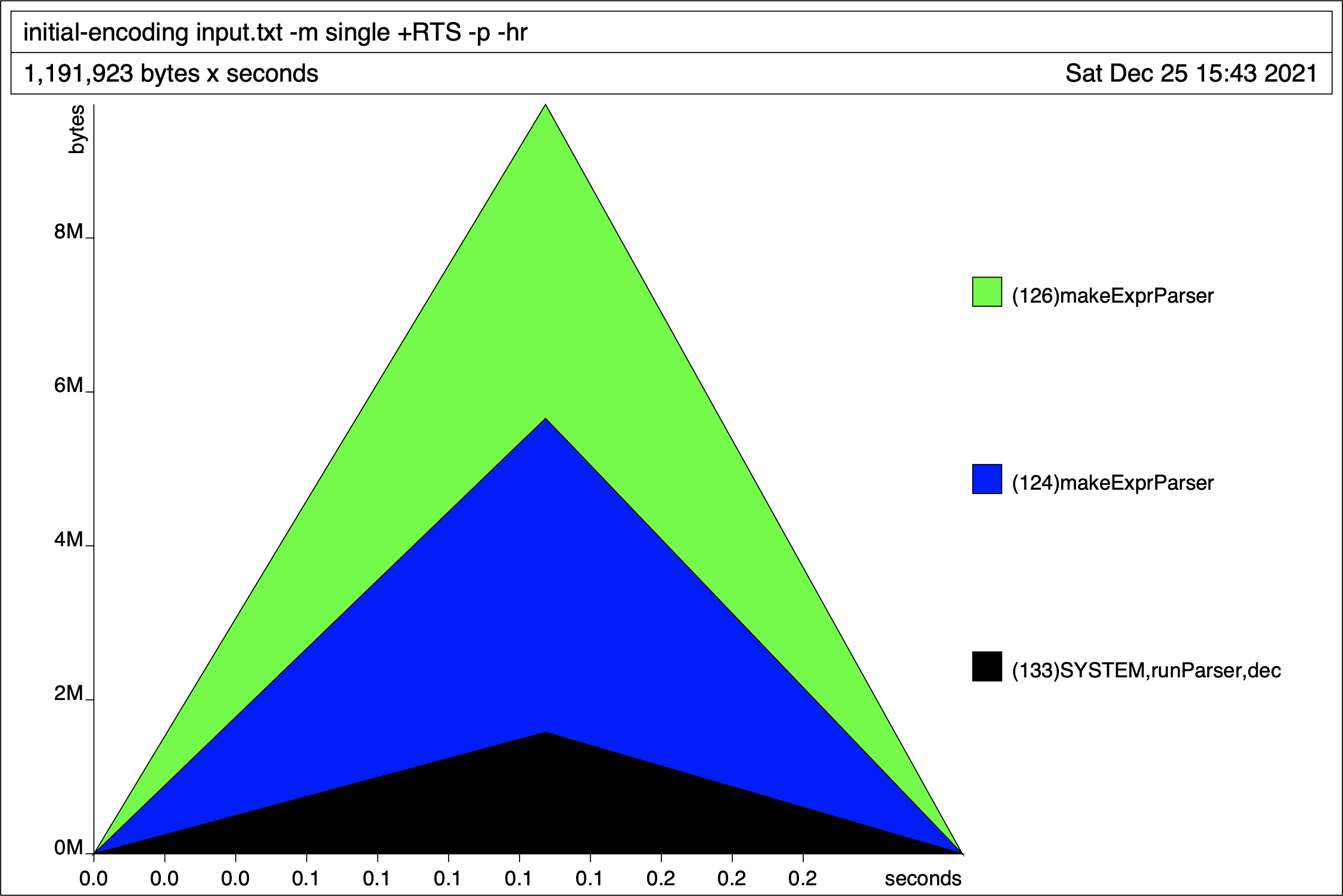
Our top-level expression parser continues growing in size until the program nears completion, presumably when the expression is finally evaluated. To further pinpoint the leaky methods, we re-run the heap generation by cost-centre stack to get:
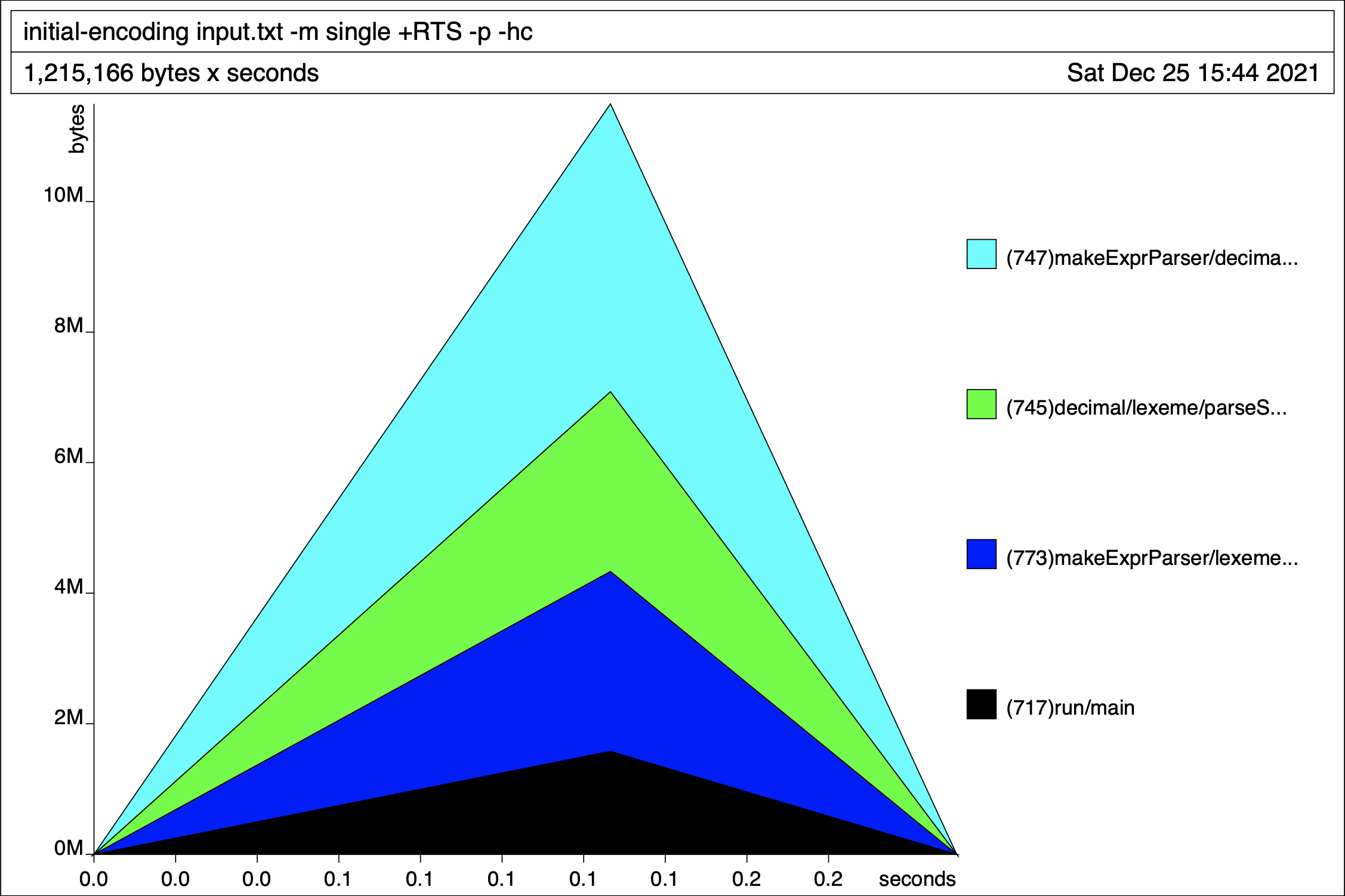
Even our straightforward lexing functions are holding on to memory. The laziness and left associative nature of our grammar hints that we may be dealing with a thunk stack reminiscient of foldl. This implies we could fix the issue by evaluating our data strictly with e.g. deepseq. The problem is unfortunately deeper than this though. Consider the definition of InfixL’s parser:
pInfixL :: MonadPlus m => m (a -> a -> a) -> m a -> a -> m a
pInfixL op p x = do
f <- op
y <- p
let r = f x y
pInfixL op p r <|> return rBecause this implementation uses the backtracking alternative
operator (<|>), we must also hold onto each
<|> return r in memory “just in case” we need to
use it. Since we are working with a left-factored
grammar, we can drop the alternatives and apply strictness with a
custom expression parser:
parseStrict :: Parser Result
parseStrict = term >>= expr
where
expr t = do
op <- M.option Nothing $ Just <$> ops
case op of
Just OpAdd -> nest t asInt EInt EAdd
Just OpSub -> nest t asInt EInt ESub
Just OpAnd -> nest t asBool EBool EAnd
Just OpOr -> nest t asBool EBool EOr
_ -> pure t
nest
:: forall a
. Result
-> (Result -> Either Text a)
-> (a -> Expr)
-> (Expr -> Expr -> Expr)
-> Parser Result
nest t cast f bin = do
t' <- term
a <- either (fail . unpack) pure do
lhs <- cast t
rhs <- cast t'
toResult $ bin (f lhs) (f rhs)
a `deepseq` expr a
term = do
p <- M.option Nothing $ Just <$> symbol "("
if isJust p then (term >>= expr) <* symbol ")" else
RInt <$> integer <|> RBool <$> booleanThis implementation runs marginally faster and uses a constant amount of memory:
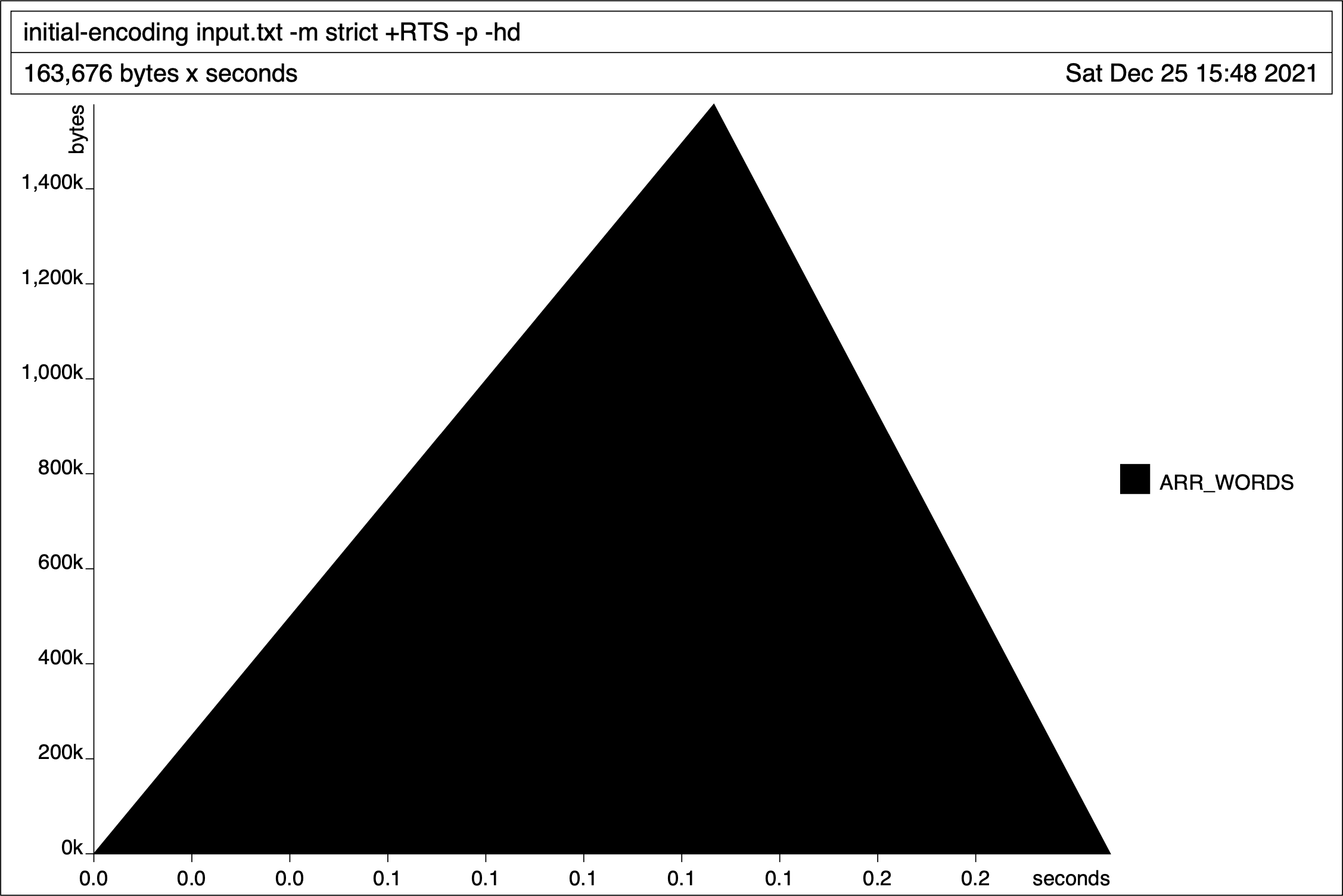
ARR_WORDS corresponds to the ByteString
constructor and is unavoidable so long as we use megaparsec.
To get a better sense of where runtime tends to reside, let’s re-run our newly strict implementation on our 10,000,000 file again alongside a time profile:
echo {1..10000000} | sed 's/ / + /g' > input.txt
cabal run --enable-profiling exe:initial-encoding -- \
input.txt -m strict +RTS -pspace Text.Megaparsec.Lexer Text/Megaparsec/Lexer.hs:(68,1)-(71,44) 54.9 57.3
decimal Text.Megaparsec.Char.Lexer Text/Megaparsec/Char/Lexer.hs:363:1-32 24.7 21.4
lexeme Text.Megaparsec.Lexer Text/Megaparsec/Lexer.hs:87:1-23 12.6 15.7
ops Parser.Utils src/Parser/Utils.hs:(69,1)-(74,3) 2.6 2.7
toResult Parser.Initial src/Parser/Initial.hs:(62,1)-(79,29) 2.3 2.2
run Main app/Main.hs:(42,1)-(54,58) 1.6 0.6
readTextDevice Data.Text.Internal.IO libraries/text/src/Data/Text/Internal/IO.hs:133:39-64 1.3 0.0Surprisingly, the vast majority of time (roughly 95%) is spent parsing. As such, we won’t worry ourselves about runtime any further.
Type Safety
Let’s next explore how we can empower library users with a stricter
version of the Expr monotype. In particular, we want to
prohibit construction of invalid expressions. A common strategy is to
promote our ADT to a GADT:
data GExpr a where
GInt :: Integer -> GExpr Integer
GBool :: Bool -> GExpr Bool
GAdd :: GExpr Integer -> GExpr Integer -> GExpr Integer
GSub :: GExpr Integer -> GExpr Integer -> GExpr Integer
GAnd :: GExpr Bool -> GExpr Bool -> GExpr Bool
GOr :: GExpr Bool -> GExpr Bool -> GExpr BoolBy virtue of working with arbitrary, potentially mis-typed input,
we must eventually perform some form of type-checking on our
input. To get the GADT representation working requires additional
machinery like existential datatypes and Rank2Types. The
end user of our library reaps the benefits though, acquiring a
strongly-typed representation of our AST:
data Wrapper = forall a. Show a => Wrapper (GExpr a)
parseGadt :: Parser Wrapper
parseGadt = term >>= expr
where
...
nest
:: forall b
. Show b
=> Wrapper
-> (forall a. GExpr a -> Either Text (GExpr b))
-> (b -> GExpr b)
-> (GExpr b -> GExpr b -> GExpr b)
-> Parser Wrapper
nest (Wrapper t) cast f bin = do
Wrapper t' <- term
case (cast t, cast t') of
(Right lhs, Right rhs) -> do
let z = eval $ bin lhs rhs
z `seq` expr (Wrapper $ f z)
(Left e, _) -> fail $ unpack e
(_, Left e) -> fail $ unpack eWe hide the full details here (refer to the linked Github
repository for the full implementation), but note the changes are
minimal outside of the signatures/data types required to make our
existentially quantified type work. Users of the parser can now unwrap
the Wrapper type and resume like normal.
This is an arguable "improvement" considering convenience
takes a dramatic hit. It is awkward working with the
Wrapper type.
Expression Problem
Lastly comes the expression problem, and one that is fundamentally unsolvable given our current implementation. By nature of (G)ADTs, all data-types are closed. It is not extensible since that would break any static type guarantees around e.g. pattern matching. To fix this (and other problems still present in our implementation), we contrast our initial encoding to that of tagless final.
Tagless Final
Let’s re-think our GADT example above and refactor it into a typeclass:
class Symantics repr where
eInt :: Integer -> repr Integer
eBool :: Bool -> repr Bool
eAdd :: repr Integer -> repr Integer -> repr Integer
eSub :: repr Integer -> repr Integer -> repr Integer
eAnd :: repr Bool -> repr Bool -> repr Bool
eOr :: repr Bool -> repr Bool -> repr BoolThis should look familiar. Instances of GExpr have
been substituted by a parameter repr of kind
* -> *. Kiselyov describes typeclasses used this way
as a means of defining a class of interpreters. An example
interpreter could look like evaluation from before:
newtype Eval a = Eval {runEval :: a}
instance Symantics Eval where
eInt = Eval
eBool = Eval
eAdd (Eval lhs) (Eval rhs) = Eval (lhs + rhs)
eSub (Eval lhs) (Eval rhs) = Eval (lhs - rhs)
eAnd (Eval lhs) (Eval rhs) = Eval (lhs && rhs)
eOr (Eval lhs) (Eval rhs) = Eval (lhs || rhs)To belabor the similarities between the two a bit further, compare the following two examples side-by-side:
let expr = foldl' eAdd (eInt 0) $ take count (eInt <$> [1..])
let expr = foldl' EAdd (EInt 0) $ take count (EInt <$> [1..])Outside of some capitalization, the encodings are exactly the same.
Considering these similarities, it’s clear type safety is not a
concern like it was with Expr. This new paradigm also
allows us to write both an implementation that parallels the memory
usage of above as well as a proper
solution to the expression problem. To follow along though first
requires a quick detour into leibniz equalities.
Leibniz Equality
Leibniz equality states that two objects are equivalent provided they can be substituted in all contexts without issue. Consider the definition provided by the eq package:
newtype a := b = Refl {subst :: forall c. c a -> c b}Here we are saying two types a and b
actually refer to the same type if it turns out that
simultaneously
• Maybe a ~ Maybe b
• Either String a ~ Either String b
• Identity a ~ Identity b
• ...and so on, where ~ refers to equality
constraints. Let’s clarify further with an example. Suppose we had
types A and B and wanted to ensure they were
actually the same type. Then there must exist a function
subst with signature c A -> c B for
all c. What might that function look like? It turns
out there is only one acceptable choice: id.
This might not seem particularly valuable at first glance, but what it does permit is a means of proving equality at the type-level and in a way Haskell’s type system respects. For instance, the following is valid:
>>> import Data.Eq.Type ((:=)(..))
>>> :set -XTypeOperators
-- Type-level equality is reflexive. I can prove it since
-- `id` is a suitable candidate for `subst`.
>>> refl = Refl id
>>> :t refl
refl :: b := b
-- Haskell can verify our types truly are the same.
>>> a = refl :: (Integer := Integer)
>>> a = refl :: (Integer := Bool)
<interactive>:7:5: error:
• Couldn't match type ‘Integer’ with ‘Bool’We can also prove less obvious things at the type-level and take advantage of this later on. As an exercise, consider how you might express the following:
functionEquality
:: a1 := a2
-> b1 := b2
-> (a1 -> b1) := (a2 -> b2)That is, if a1 and a2 are the same types,
and b1 and b2 are the same types, then
functions of type a1 -> b1 can equivalently be
expressed as functions from a2 -> b2.
Answer
I suggest reading from the bottom up to better understand why this works.
import Data.Eq.Type ((:=)(..), refl)
newtype F1 t b a = F1 {runF1 :: t := (a -> b)}
newtype F2 t a b = F2 {runF2 :: t := (a -> b)}
functionEquality
:: forall a1 a2 b1 b2
. a1 := a2
-> b1 := b2
-> (a1 -> b1) := (a2 -> b2)
functionEquality
(Refl s1) -- s1 :: forall c. c a1 -> c a2
(Refl s2) -- s2 :: forall c. c b1 -> c b2
= runF2 -- (a1 -> b1) := (a2 -> b2)
. s2 -- F2 (a1 -> b1) a2 b2
. F2 -- F2 (a1 -> b1) a2 b1
. runF1 -- (a1 -> b1) := (a2 -> b1)
. s1 -- F1 (a1 -> b1) b1 a2
. F1 -- F1 (a1 -> b1) b1 a1
$ refl -- (a1 -> b1) := (a1 -> b1)Dynamics
Within our GADTs example, we introduced data type
Wrapper to allow us to pass around GADTs of internally
different type (e.g. GExpr Integer vs.
GExpr Bool) within the same context. We can do something
similar via Dynamics in the tagless final world. Though
we could use the already available dynamics
library, we’ll build our own for exploration’s sake.
First, let’s create a representation of the types in our grammar:
class Typeable repr where
pInt :: repr Integer
pBool :: repr Bool
newtype TQ t = TQ {runTQ :: forall repr. Typeable repr => repr t}
instance Typeable TQ where
pInt = TQ pInt
pBool = TQ pBoolTQ takes advantage of polymorphic constructors to
allow us to wrap any compatible Typeable member function
and “reinterpret” it as something else. For example, we can create new
Typeable instances like so:
newtype AsInt a = AsInt (Maybe (a := Integer))
instance Typeable AsInt where
pInt = AsInt (Just refl)
pBool = AsInt Nothing
newtype AsBool a = AsBool (Maybe (a := Bool))
instance Typeable AsBool where
pInt = AsBool Nothing
pBool = AsBool (Just refl)We can then use TQ to check if something is of the
appropriate type:
>>> import Data.Maybe (isJust)
>>> tq = pInt :: TQ Integer
>>> case runTQ tq of AsInt a -> isJust a
True
>>> case runTQ tq of AsBool a -> isJust a
FalseEven more interestingly, we can bundle this type representation
alongside a value of the corresponding type, yielding our desired
Dynamic:
import qualified Data.Eq.Type as EQ
data Dynamic repr = forall t. Dynamic (TQ t) (repr t)
class IsDynamic a where
type' :: forall repr. Typeable repr => repr a
lift' :: forall repr. Symantics repr => a -> repr a
cast' :: forall repr t. TQ t -> Maybe (t := a)
instance IsDynamic Integer where
type' = pInt
lift' = eInt
cast' (TQ t) = case t of AsInt a -> a
instance IsDynamic Bool where
type' = pBool
lift' = eBool
cast' (TQ t) = case t of AsBool a -> a
toDyn :: forall repr a. IsDynamic a => Symantics repr => a -> Dynamic repr
toDyn = Dynamic type' . lift'
fromDyn :: forall repr a. IsDynamic a => Dynamic repr -> Maybe (repr a)
fromDyn (Dynamic t e) = case t of
(cast' -> r) -> do
r' <- r
pure $ EQ.coerce (EQ.lift r') e>>> a = toDyn 5 :: Dynamic Expr
>>> runExpr <$> fromDyn a :: Maybe Integer
Just 5By maintaining a leibniz equality within our Dynamic
instances (i.e. AsInt), we can internally coerce the
wrapped value into the actual type we care about. With this background
information in place, we can finally devise an expression parser
similar to the parser we’ve written using initial encoding:
parseStrict
:: forall repr
. NFData (Dynamic repr)
=> Symantics repr
=> Parser (Dynamic repr)
parseStrict = term >>= expr
where
expr :: Dynamic repr -> Parser (Dynamic repr)
expr t = do
op <- M.option Nothing $ Just <$> ops
case op of
Just OpAdd -> nest t eAdd OpAdd
Just OpSub -> nest t eSub OpSub
Just OpAnd -> nest t eAnd OpAnd
Just OpOr -> nest t eOr OpOr
_ -> pure t
nest
:: forall a
. IsDynamic a
=> Dynamic repr
-> (repr a -> repr a -> repr a)
-> Op
-> Parser (Dynamic repr)
nest t bin op = do
t' <- term
case binDyn bin t t' of
Nothing -> fail $ "Invalid operands for `" <> show op <> "`"
Just a -> a `deepseq` expr a
term :: Parser (Dynamic repr)
term = do
p <- M.option Nothing $ Just <$> symbol "("
if isJust p then (term >>= expr) <* symbol ")" else
toDyn <$> integer <|> toDyn <$> booleanInterpretations
So far we’ve seen very little benefit switching to this strategy despite the level of complexity this change introduces. Here we’ll pose a question that hopefully makes at least one benefit more obvious. Suppose we wanted to interpret the parsed expression in two different ways. First, we want a basic evaluator, and second we want a pretty-printer. In our initial encoding strategy, the evaluator has already been defined:
eval :: GExpr a -> aWe say eval is one possible interpreter over
GExpr. It takes in GExprs and reduces them
into literal values. How would a pretty printer work? One candidate
interpreter could look as follows:
pPrint :: GExpr a -> Text
pPrint (GInt e) = pack $ show e
pPrint (GBool e) = pack $ show e
pPrint (GAdd lhs rhs) = "(" <> pPrint lhs <> " + " <> pPrint rhs <> ")"
...Unfortunately using this definition requires fundamentally changing
how our GADT parser works. parseGadt currently makes
certain optimizations based on the fact only eval has
been needed so far, reducing the expression as we traverse the input
stream. Generalizing the parser to take in any function of signature
forall b. (forall a. GExpr a) -> b (i.e. the signature
of some generic interpreter) would force us to retain memory or accept
additional arguments to make our function especially generic to
accommodate.2
On the other hand, our tagless final approach expects multiple
interpretations from the outset. We can define a newtype
like
newtype PPrint a = PPrint {runPPrint :: a}
instance Symantics PPrint where
eInt = PPrint . pack . show
eBool = PPrint . pack . show
eAdd (PPrint lhs) (PPrint rhs) = PPrint $ "(" <> lhs <> " + " <> rhs <> ")"
...and interpret our
parseStrict :: forall repr. Symantics repr => Parser (Dynamic repr)Parser as a Dynamic PPrint instead of a
Dynamic Eval without losing any previously acquired
gains.
Expression Revisited
There does exist a major caveat with our tagless final
interpreters. If owning a single Dynamic instance, how
exactly are we able to interpret this in multiple ways? After all, a
Dynamic cannot be of type Dynamic Eval
and Dynamic PPrint. What we’d like to be able to
do is maintain a generic Dynamic repr and reinterpret it
at will.
One solution comes in the form of another newtype
around a polymorphic constructor:
newtype SQ a = SQ {runSQ :: forall repr. Symantics repr => repr a}
instance Symantics SQ where
eInt e = SQ (eInt e)
eBool e = SQ (eBool e)
eAdd (SQ lhs) (SQ rhs) = SQ (eAdd lhs rhs)
eSub (SQ lhs) (SQ rhs) = SQ (eSub lhs rhs)
eAnd (SQ lhs) (SQ rhs) = SQ (eAnd lhs rhs)
eOr (SQ lhs) (SQ rhs) = SQ (eOr lhs rhs)We can then run evaluation and pretty-printing on the same entity:
data Result = RInt Integer | RBool Bool
runBoth :: Dynamic SQ -> Maybe (Result, Text)
runBoth d = case fromDyn d of
Just (SQ q) -> pure ( case q of Eval a -> RInt a
, case q of PPrint a -> a
)
Nothing -> case fromDyn d of
Just (SQ q) -> pure ( case q of Eval a -> RBool a
, case q of PPrint a -> a
)
Nothing -> NothingThis has an unintended side effect though. By using
SQ, we effectively close our type universe. Suppose we
now wanted to extend our Symantics type with a new
multiplication operator (*). We could do so by writing
typeclass:
class MulSymantics repr where
eMul :: repr Integer -> repr Integer -> repr Integer
instance MulSymantics Eval where
eMul (Eval lhs) (Eval rhs) = Eval (lhs * rhs)
instance MulSymantics PPrint where
eMul (PPrint lhs) (PPrint rhs) = PPrint $ "(" <> lhs <> " * " <> rhs <> ")"Naturally we also need to extend our parser to be aware of the new operator as well. To avoid diving yet further into the weeds, we do not do that here.
But this typeclass is excluded from our SQ type. We’re
forced to write yet another SQ-like wrapper, e.g.
newtype MSQ a = MSQ {runMSQ :: forall repr. MulSymantics repr => repr a}just to keep up. This in turn forces us to redefine all functions
that operated on SQ.
Copy Symantics
We can reformulate this more openly, abandoning any sort of
Rank2 constructors within our newtypes by
choosing to track multiple representations simultaneously:
data SCopy repr1 repr2 a = SCopy (repr1 a) (repr2 a)
instance (Symantics repr1, Symantics repr2)
=> Symantics (SCopy repr1 repr2) where
eInt e = SCopy (eInt e) (eInt e)
eBool e = SCopy (eBool e) (eBool e)
eAdd (SCopy a1 a2) (SCopy b1 b2) = SCopy (eAdd a1 b1) (eAdd a2 b2)
eSub (SCopy a1 a2) (SCopy b1 b2) = SCopy (eSub a1 b1) (eSub a2 b2)
eAnd (SCopy a1 a2) (SCopy b1 b2) = SCopy (eAnd a1 b1) (eAnd a2 b2)
eOr (SCopy a1 a2) (SCopy b1 b2) = SCopy (eOr a1 b1) (eOr a2 b2)
instance (MulSymantics repr1, MulSymantics repr2)
=> MulSymantics (SCopy repr1 repr2) where
eMul (SCopy a1 a2) (SCopy b1 b2) = SCopy (eMul a1 b1) (eMul a2 b2)As we define new classes of operators on our Integer
and Bool types, we make SCopy an instance of
them. We can then “thread” the second representation throughout our
function calls like so:
runEval'
:: forall repr
. Dynamic (SCopy Eval repr)
-> Maybe (Result, Dynamic repr)
runEval' d = case fromDyn d :: Maybe (SCopy Eval repr Integer) of
Just (SCopy (Eval a) r) -> pure (RInt a, Dynamic pInt r)
Nothing -> case fromDyn d :: Maybe (SCopy Eval repr Bool) of
Just (SCopy (Eval a) r) -> pure (RBool a, Dynamic pBool r)
Nothing -> Nothing
runPPrint'
:: forall repr
. Dynamic (SCopy PPrint repr)
-> Maybe (Text, Dynamic repr)
runPPrint' d = case fromDyn d :: Maybe (SCopy PPrint repr Text) of
Just (SCopy (PPrint a) r) -> pure (a, Dynamic pText r)
Nothing -> Nothing
runBoth'
:: forall repr
. Dynamic (SCopy Eval (SCopy PPrint repr))
-> Maybe (Result, Text, Dynamic repr)
runBoth' d = do
(r, d') <- runEval' d
(p, d'') <- runPPrint' d'
pure (r, p, d'')Notice each function places a Dynamic repr of unknown
representation in the last position of each return tuple. The caller
is then able to interpret this extra repr as they wish,
composing them in arbitrary ways (e.g. runBoth').
Limitations
The expression problem is only partially solved with our
Dynamic strategy. If for instance we wanted to add a new
literal type, e.g. a String, we would unfortunately need
to append to the Typeable and Dynamic
definitions to support them. The standard dynamics
package only allows monomorphic values so in this sense we are stuck.
If only needing to add additional functionality to the existing set of
types though, we can extend at will.
Conclusion
I was initially hoping to extend this post further with a discussion around explicit sharing as noted here, but this post is already getting too long. I covered only a portion of the topics Oleg Kiselyov wrote about, but covered at least the majority of topics I’ve so far been exploring in my own personal projects. I will note that the tagless final approach, while certainly useful, also does add a fair level of cognitive overhead in my experience. Remembering the details around dynamics especially is what prompted me to write this post to begin with.